P3230 [HNOI2013]比赛

首先显然想到的是暴力搜索，爆搜的方式就是 1v2->1v3...->1vN，然后 2V3...直至结尾。

然后很明显要剪枝，我们用 dfs(nowt,nowm) 表示现在是编号为 nowt 的战队打编号为 nowm ， now[x] 表示编号为 x 的战队的当前得分， a[x] 表示编号为 x 的战队的最终得分。给出下面几个剪枝方案：

如果这个现在的得分超过了这个队的最终得分，因为即使输了也不会扣分，所以无论如何都无法满足最终的得分，那么此时应该退出。
```
  if (now[nowt] > a[nowt]) return;
```
如果此时的得分少的可怜，即使后面全赢这个队伍也得不到预期得分，那么此时应该退出。
```
if(now[nowt] + (n - nowm + 1) * 3 < a[nowt]) return 0 ;
```

下面的剪枝就比较难想了。

记忆化，这题很重要的性质就是如果人数和分数一定，那么方案数也一定，和每个人的具体得分无关，用哈希存储之后记忆化。

if(nowm > n)  
	{
		for(int i = nowt + 1 ; i <= n ; i ++) hashh[i] = a[i] - now[i] ;
		sort(hashh + nowt + 1 , hashh + n + 1 , cmp) ;
		ll ha = 0 ;
		for(int i = nowt + 1 ; i <= n ; i ++)	ha = ha * 97 + hashh[i] ; 
		if(hash.find(ha) != hash.end()) return hash[ha] ;
		else return hash[ha] = dfs(nowt + 1 , nowt + 2) ;  
	}

如果总得分是 sum，胜利场数是 win，平局场数是 draw，那么有

$\begin{cases}win + draw = \dfrac{n \times (n+1)}{2}\\ 3 \times win+2\times draw=sum\end{cases}$

解得

$\begin{cases}win = sum-n \times (n+1)\\ draw=\dfrac {n \times(n-1)}{2}-win\end{cases}$

手动解得答案即可。
```
win = sum - n * (n - 1) , draw = n * (n - 1) / 2 - win ;
```
解出答案后我们就可以以此来控制这个队胜利和平局的场数，也就是说如果现在的胜利或者平局场数超过了最后的胜利或平局场数，应该退出。
就像这样：
```
if(now[nowt] + 3 <= a[nowt] && win)
```
先搜得分大的一定状态少，为什么呢，因为得分小的比较容易被得分大的影响，也就是先搜得分大的那么得分小的的状态一定比较少。

也就是我们更愿意第一图的样子而不是第二图。

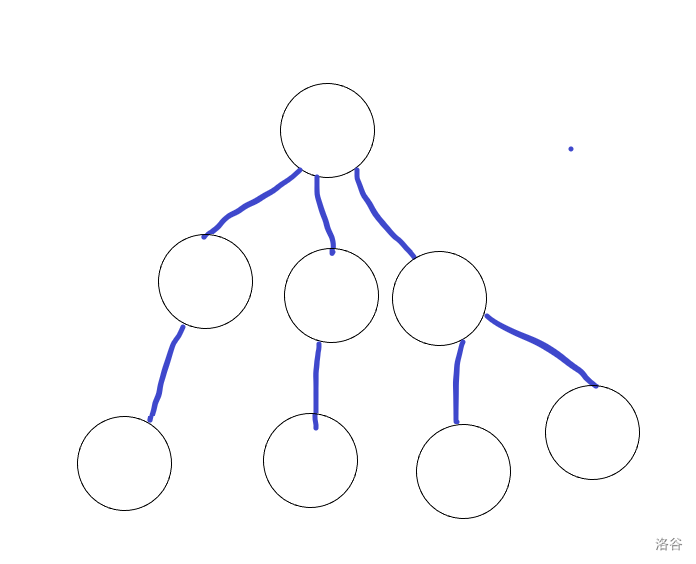
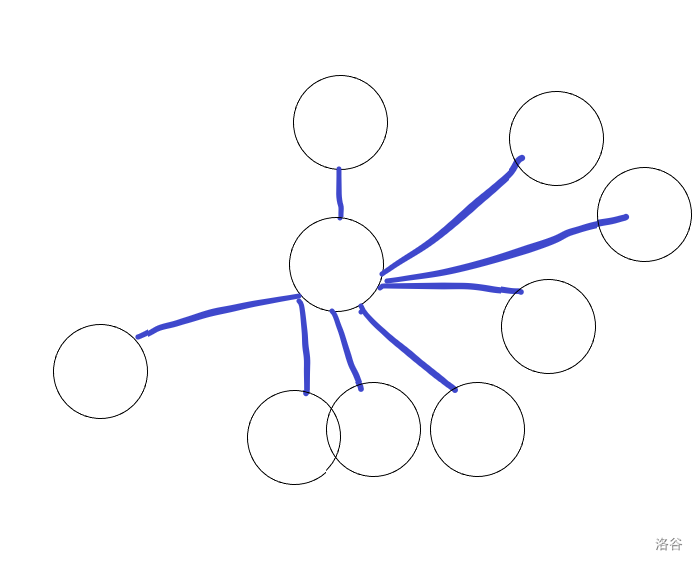
所以先搜最终得分大的。
```
sort(a + 1 , a + n + 1 , cmp) ;
```

至此，剪枝完毕，核心代码已经给出，剩下的实现难度不高。

~~其实可以利用ssh直接在赛场上过的~~

Cocoly1990's Blog

SP32192 SUMMATION - SUMMATION