Cocoly1990's Blog

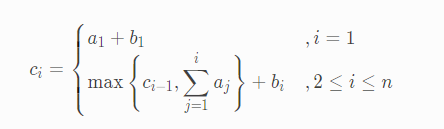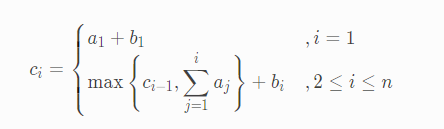
很显然对于上式，要使得每一个 $c_i$ 尽可能小，因为 $c_{i-1}$ 尽可能小，$c_i$ 也会尽可能小。

作如下考虑

$x,x,x,x,j,i,x,x,x,x$

$x,x,x,x,i',j',x,x,x,x$

假设有两个相邻的位置 $c_i,c_j$，在什么情况下交换 $c_i,c_j$ 能使 $c_j$ 减小。

令 $sum_i=\sum\limits_{j=1}^i a_j$.

那么有

$c_j=max(c_{j-1}+b_j,sum_j+b_j)$

$c_i=max(c_{j},sum_i)+b_i=max(c_{j-1}+b_j+b_i,sum_j+b_j+b_i,sum_i+b_i)$

交换后有

$c_{i'}=max(c_{j-1}+b_i,sum_i-a_j+b_i)$

$c_{j'}=max(c_{j-1}+b_i+b_j,sum_i-a_j+b_i+b_j,sum_i+b_j)$

那么 $c_{j'} \ge c_i$ 这说明 $j$ 在 $i$ 前面。

首先，如果 $c_i=c_{j-1}+b_j+b_i$，那么 $c_{j'} \ge c_i$ 一定成立（很好理解吧）。

所以在比较 $c_{j'},c_i$ 时可以忽略 $c_{j-1}+b_j+b_i$.

所以只需要比较

$max(sum_i-a_j+b_i+b_j,sum_i+b_j) \ge max(sum_j+b_j+b_i,sum_i+b_i)$

$max(sum_i-a_j,sum_i-b_i) \ge max(sum_j,sum_i-b_j)$

然后再减 $sum_i$，注意 $sum_j-sum_i=-a_i$

$max(-a_j,-b_i) \ge max(-a_i,-b_j)$

$min(a_j,b_i) \le min(a_i,b_j)$

也就是说，如果上式满足，则有 $j$ 在 $i$ 前面。

但不具备传递性，也就是假设有 $j$ 在 $i$ 前面且 $k$ 在 $j$ 前面，不一定有 $k$ 在
$i$ 前面。

分类讨论

1. $a_i \le b_i$ 则有 $a_j \le a_i$且 $a_j \le b_j$ 这一组按$a$升序排列。

2. $a_i > b_i$ 则有 $b_j \ge b_i$或$b_j \ge a_j$ 这一组按$b$降序排列。

如果 $\dfrac{a_i-b_i}{abs(a_i-b_i)}\le 0$，分到$1$.

如果 $\dfrac{a_i-b_i}{abs(a_i-b_i)}> 0$，分到$2$.

代码就很好写了，记得long long。