AT2167 [AGC006F] Blackout
题意简述
有一张 的网格,一开始共有 个格子被涂成黑色,其它所有格子都是白色的。
如果存在三个正整数 (),满足 和 都是黑色的,那么就可以将 涂成黑色。
求最多能使棋盘上有多少个黑色的格子。
思路
以下部分内容来自于教练的讲义,融入了笔者的思考
认真思考,我们可以发现以下性质
如果 和 中任两个是黑色的,则第三个是黑色的。
更进一步的是,如果对任意 ,都存在 满足 和 同时为黑,那么 也是黑的。
我们不妨把一个黑色的格子当做两个元素之间产生关联。这种关联是单向的,即 是黑的不能得出 也是黑的。
考虑在膜 的意义下建图
我们假设有三个互不相交的非空集合正解 他们分别用 ,每个元素必然存在于其中一个点集。
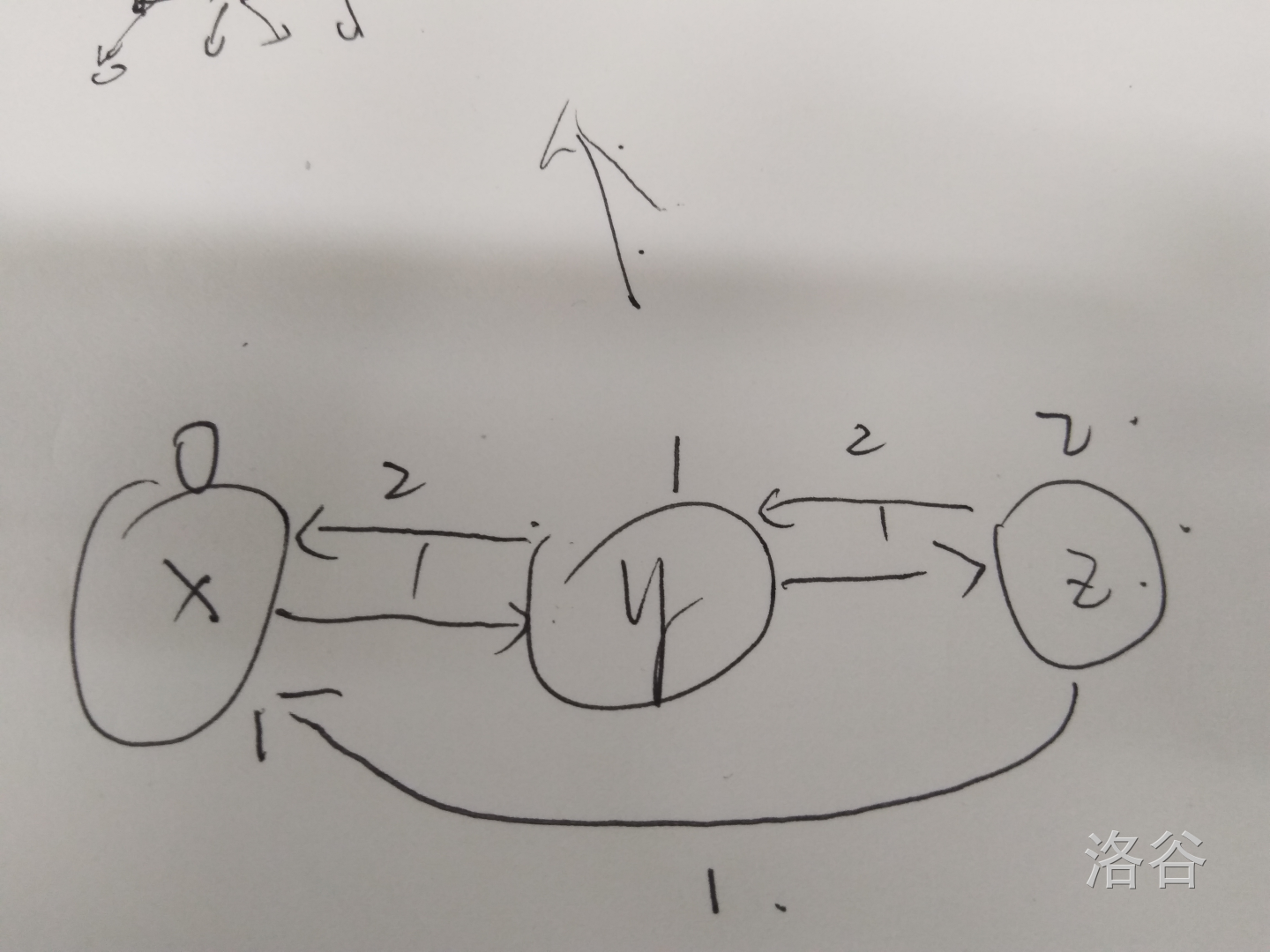
我们可以假设 到 , 到 的距离为.
那么在膜 意义下,各集合之间的距离就可以算出,如 到 的距离应该为 ,因为在膜 意义下
显然对于不同连通块,我们可以分开处理。我们可以分成一下三种情况处理。同样显然的是,每两点存在联系,就表明存在一个黑块。
-
如果一个连通块的点集可以被划分为两个不相交的集合,且只有其中一个集合的点向另一个集合连边,每个集合内部没有连边,那么这个连通块不能产生新的边。此时仅需统计边数即可,值得注意的是,因为我们建的是有向图,所以统计出来的边数除以 即可。
-
如果一个连通块的点集可以被划分为三个不相交的集合 ,且 中的每个点都与 中的至少一个点连边,其他集合间的关系相同。那么这个连通块的最终状态为 中所有点向 中所有点连边,其他两个集合关系相同。最终边数为 。
-
如果一个连通块不符合上面说的任意一种情况,如集合内部有连边,则最终状态为集合内部所有点对之间都有连边(包括自环)。最终边数为点数平方。
具体怎么判断呢,我们可以进行染色,对于每个节点,我们用 记录下它所在的集合(同上图三个集合),对于任意两个联通点,如果 col[v] != (col[u] + e[j].w) % 3 则说明他们不分属两个集合,即集合内有边相连。对于上述 仅需判断是否三个集合内都有点即可。
综合时间复杂度 ,可以通过本题,当然了你不吸氧手写队列也并不复杂。

还算过得去/cy
code
#include<bits/stdc++.h>
#define Maxn 100007
#define ll long long
using namespace std ;
struct Edge
{
int to , w , next ;
}e[Maxn << 1] ;
int head[Maxn] , col[Maxn] , cnt[3] , tot , n , m , check , edgecnt ;
ll ans ;
bool vis[Maxn] ;
queue <int> q ;
void add(int x , int y , int w)
{
e[++ tot].to = y , e[tot].next = head[x] , head[x] = tot , e[tot].w = w ;
}
void clear(queue<int>& q)
{
queue<int> empty ;
swap(empty , q) ;
}
int main()
{
int u , v ;
cin >> n >> m ;
for(int i = 1 ; i <= m ; i ++)
{
cin >> u >> v ;
add(u , v , 1) ;
add(v , u , 2) ;
}
for(int i = 1 ; i <= n ; i ++)
if(! vis[i])
{
check = edgecnt = cnt[0] = cnt[1] = cnt[2] = 0 ;
clear(q) ; q.push(i) ;
vis[i] = 1 ;
while(! q.empty())
{
u = q.front() ;
q.pop() ;
++ cnt[col[u]] ;
for(int j = head[u] ; j ; j = e[j].next)
{
++ edgecnt ;
v = e[j].to ;
if(vis[v])
if(col[v] != (col[u] + e[j].w) % 3) check = 1 ;
if(! vis[v])
{
vis[v] = 1 ;
col[v] = (col[u] + e[j].w) % 3 ;
q.push(v) ;
}
}
}
if(check) ans += 1ll * (cnt[0] + cnt[1] + cnt[2]) * (cnt[0] + cnt[1] + cnt[2]) ;
else if(cnt[0] && cnt[1] && cnt[2]) ans += 1ll * cnt[0] * cnt[1] + 1ll * cnt[1] * cnt[2] + 1ll * cnt[2] * cnt[0] ;
else ans += edgecnt >> 1 ;
}
cout << ans ;
return 0 ;
}